Cold-rolled steel plate is a low-carbon structural steel produced by further rolling hot-rolled steel plate at room temperature or near room temperature.
Cold-rolled steel plate itself does not refer to a specific grade; cold rolling is a steel processing technique. Steel plates processed through cold rolling offer three key advantages:
First, they exhibit excellent surface quality, high finish, standardized thickness dimensions, and precise, uniform tolerances.
Second, the cold rolling process induces work hardening, resulting in high plate strength and surface hardness.
Third, excellent plasticity and formability, making it particularly suitable for applications requiring good stamping, bending, and other processing properties.
The advantages of cold-rolled steel sheets have established them as the mainstream material for industrial sheet metal work, especially in cabinetry and enclosure manufacturing.
This article compiles common bending structures, outlines their unfolding principles, and summarizes corresponding simple, practical, and easy-to-remember calculation methods with examples.
Unfolding Calculation for Angle Bends
Unfolding calculations for bends represent a technical barrier in sheet metal forming.
This process involves mathematically converting a three-dimensional sheet metal part into a two-dimensional flat pattern using empirical formulas—essentially the inverse of the forming process.
Its purpose is to determine precise blanking dimensions, ensuring the part meets exact design specifications for shape and dimensional accuracy after bending.
In engineering mechanics and materials science, the concept of the neutral layer indicates: during bending, the inner side of the sheet experiences compression while the outer side undergoes tension.
A layer in between experiences neither tension nor compression—this layer is termed the neutral layer. The length of the neutral layer remains constant before and after bending, making it crucial for unfolding calculations.
Theoretically, neutral layer theory can be applied to all bend development calculations, particularly for sheet metal with thickness t > 3.0 mm.
However, for cold-rolled steel sheets with thickness t ≤ 3.0 mm, neutral layer theory becomes overly complex. Consequently, for angle bend development calculations, the author recommends the bend deduction method.
Unfolding Calculation for 90° Bends
Principle of 90° Bend Deduction
The 90° bend, or right-angle bend, is the most common type. Here, we illustrate the bend deduction method used in unfolding calculations with diagrams and a calculation example.
As shown in Figure 1, the formula for calculating the unfolded length based on the bend deduction method is:
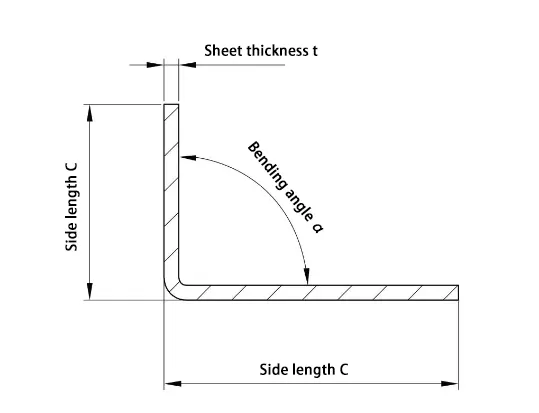
Where:
- ZL — Unfolded length;
- A, C — Outer dimensions of bend flange length;
- n — Number of bending dies;
- BD — Bend deduction value, where BD = tY (t being the sheet thickness).
Bending Coefficient and Die Selection
The bending coefficient Y is a conventional calculation constant based on empirical data, which can be validated and refined through practical bending tests.
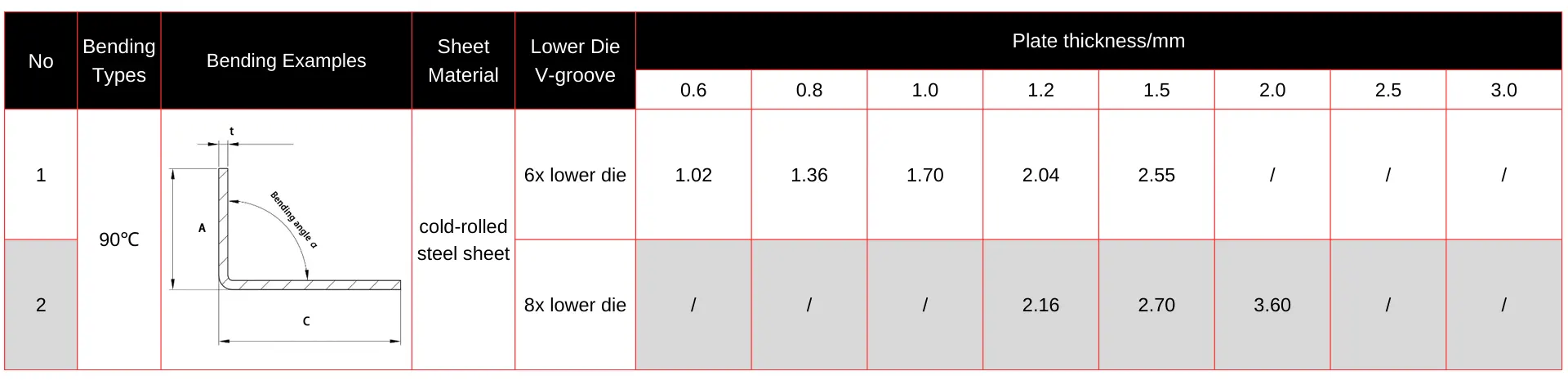
The influence factors of bending coefficient Y depend on the sheet material and the size of the lower die V-groove opening: Generally, the V-groove opening size corresponds to a simple multiple of the sheet thickness t, commonly referred to as 6x die, 8x die, and 10x die.
For example, a 6x die means the V-groove opening size equals 6 times the sheet thickness, and so on.
Typically, the relationship between the bending coefficient Y and the lower die V-groove opening size is as follows:
- 6x die: Y=1.70, suitable for sheet thicknesses 0.6–1.5mm;
- 8x die: Y=1.80, suitable for sheet thicknesses 1.2–2.0mm;
- 10x die: Y=2.0, suitable for sheet thicknesses 2.0–3.0mm.
Bending allowances for different V-groove openings and sheet thicknesses are shown in Table 1.
Example: As shown in Figure 2, the material is cold-rolled steel plate with thickness t=1.5mm.
The outer dimensions of the bend edges are A=25.0mm, C=65.0mm, E=25.0mm, F=30.0mm, all with 90° bend angles. Determine the unfolded length ZL.
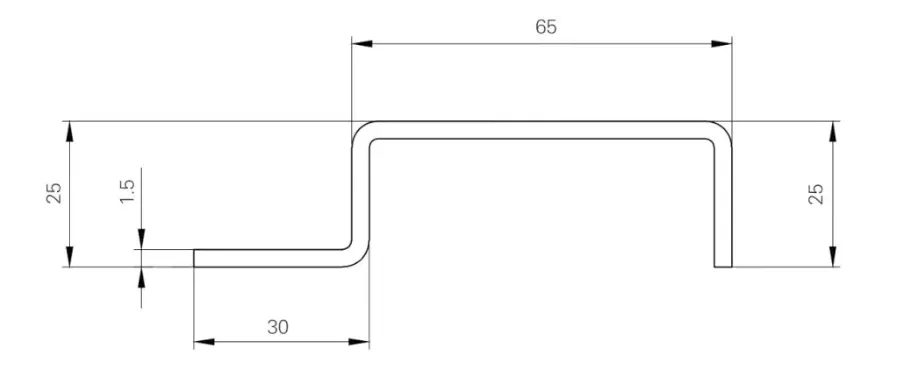
Calculation: From the diagram, three bends are required, yielding n=3 bends. With sheet thickness t=1.5mm and a 6x lower die selected, the bend allowance BD=2.55mm from Table 1. Thus, ZL=(A+C+E+F)-nBD=(25+65+25+30)-3×2.55=137.35mm.
Calculation result: The developed length ZL is 137.35 mm.
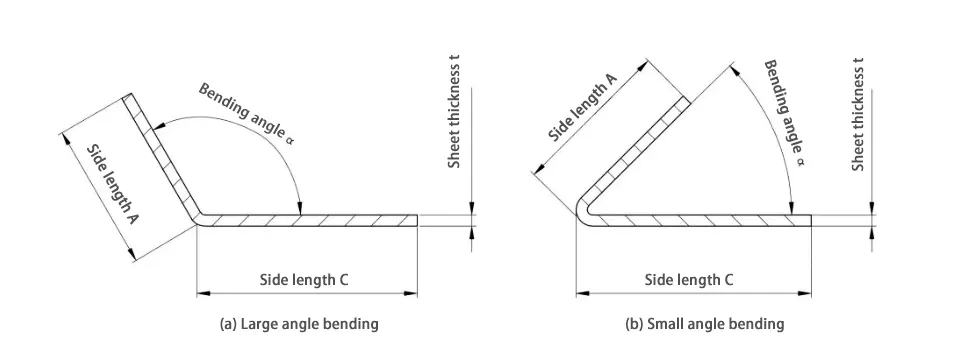
Development Calculations for Large-Angle and Small-Angle Bends
Large-angle bends typically refer to bends exceeding 90°, while small-angle bends generally denote bends less than 90°.
In practical manufacturing, development calculations for both large-angle and small-angle bends are frequently encountered. Measurement errors in the bend leg length often lead to corresponding errors in the development calculations.
Therefore, similarly based on the bend deduction method, the development formulas for large-angle and small-angle bends are derived from the aforementioned 90° bend development formula:
ZL = (A + C) – mBD
Where m is the angle coefficient, m = (180° – α) / α, and α is the bend angle.
When calculating the angle coefficient m, note: As shown in Figure 3, when α > 90°, substitute α directly into the formula. When α < 90°, substitute the complementary angle of α into the formula.
For example, when α=120°, m=(180°-120°)/120°=0.50; when α=60°, the complementary angle of 60° is 120°, thus m=(180°-120°)/120°=0.50.
Thus, it is evident that complementary bending angles share the same angle coefficient m. This method is applicable for developing calculations across various bending angles.
Development Calculation for Arc Bends
Arc Bending Method
At the process level, arc bending using a three-point bending method is essentially polygonal bending. The more sides a polygon has, the smoother the resulting arc becomes.
This method is also known as equal-cut-equal-distance polygonal bending.
The parameters for polygonal bending (i.e., arc bending) include the number of cuts, cut spacing, and angle. These parameters are determined using neutral layer theory.
Arc bending generally exhibits three structural forms, as shown in Figure 4. The diagram reveals a key characteristic: the clamping angle αj is the complementary angle to the arc angle α.
Regardless of the form, accurately determining the arc angle α is critical for unfolding calculations.
Figure 4 Schematic Diagram of Arc Bending Structures
Arc Bend Dies (Upper Die and Lower Die)
For arc bending, the recommended upper die is a straight die or standard die, while the lower die is a large-angle V-notch die with a depth of 6 to 8 times the sheet thickness (the angle of the lower die V-notch must exceed that of the upper die).
Selecting appropriate upper and lower dies, combined with precise calculations, ensures optimal arc bending results.
Arc Bending Unfolding Calculation (Abbreviated as the 5-Step Arc Calculation Method)
Given sheet thickness t, arc outer radius R, and arc angle α as shown in Figure 4, the specific steps for calculating the number of bends N, bend pitch J, and bend angle β using the 5-Step Arc Calculation Method are as follows.
Step 1: Determine the neutral layer radius Rc.
The neutral layer is typically positioned at the midpoint of the sheet thickness (i.e., 1/2 of the sheet thickness), thus Rc = R – t/2.
Step 2: Calculate the arc length Lc of the neutral layer (equivalent to the developed length of the arc).
Arc length Lc = απRc / 180°.
Step 3: Calculate the number of bends.
Calculate the number of bends based on the preset bend pitch. Round the result up to the nearest integer and confirm this as the number of bends N.
The preset bend pitch is generally 1 to 3 times the sheet thickness. Number of bends N = Lc / preset bend pitch (arc length divided by preset bend pitch).
Step 4: Calculate the bend pitch J.
Bend pitch J = Lc / N (arc length divided by number of bends).
Step 5: Calculate the bend angle β.
Bend angle β = α/N (arc angle divided by number of bends). In practice, it is recommended that both the first and last bends of an arc use a bend angle of β/2.
The 5-step arc bend calculation method can be summarized as an easy-to-remember mnemonic: Confirm radius, calculate arc length, calculate number of bends, calculate bend spacing, calculate angle.
Example: As shown in Figure 4(c), the material is cold-rolled steel plate with thickness t=1.20mm.
◊ Arc Bend Calculation Example: Bend Count, Pitch, and Angle
Given the outer radius R=43.0mm, edge angle αj=45°, and side lengths E=F=25.0mm, determine the number of bends N, bend spacing J, and angle β for this arc bend.
Calculation: Follow the 5-step arc calculation method. Retain two decimal places during the calculation process and one decimal place in the final result.
Step 1: Determine the neutral layer radius Rc of the arc.
Rc = R – t/2 = 43.0 – 1.20/2 = 42.40 mm.
Step 2: Calculate the neutral layer arc length Lc.
According to the characteristics of arc bending, the edge angle αj is the complementary angle to the arc angle α. Therefore, arc angle α = 180° – αj = 180° – 45° = 135°.
Neutral layer arc length Lc = απRc/180° = 135° × 3.14² × 42.40/180° ≈ 99.92 mm.
Step 3: Calculate the number of bending passes.
The preset blade spacing is 1 to 3 times the sheet thickness. Taking 2.5 times the sheet thickness as the preset spacing, the preset blade spacing is 3.0 mm.
Thus, the number of bends N = Lc / preset blade spacing = 99.92 / 3 ≈ 33.31 bends. Rounding up, the actual number of bends N = 34 bends.
Step 4: Calculate the bend pitch J.
Pitch J = Lc/N = 99.92/34 ≈ 2.94 mm/bend.
Step 5: Calculate the bend angle β.
β = α/N = 135°/34 ≈ 3.97°
Calculation results: Number of bends N = 34 bends, bend pitch J = 2.9 mm, angle β = 4.0°.
Conclusion
In summary, the unfolding calculations for cold-rolled steel plate bending—whether employing the bending deduction method or the neutral layer theory—are mutually compatible, complementary, and verifiable.
Accurate bending unfolding calculations not only ensure production schedules and product processing precision/quality but also serve deeper functions and significance.
On one hand, calculations provide a basis for selecting upper dies and lower dies, as well as determining a rational bending sequence. This avoids repeated trial runs and adjustments, thereby enhancing production efficiency.
On the other hand, calculations support and validate the design and process of complex structures—particularly those involving multi-die bending and irregular bending combinations.
This provides guidance and early warnings for subsequent processing and assembly operations.
FAQ
What is the difference between cold-rolled steel plate and a specific steel grade?
Cold-rolled steel plate does not denote a specific material grade. It refers to a processing method in which hot-rolled steel is further rolled at room temperature or near room temperature. The resulting material typically exhibits improved surface finish, tighter thickness tolerances, higher strength due to work hardening, and better formability compared with hot-rolled steel.
Why is cold-rolled steel widely used in sheet metal bending applications?
Cold-rolled steel is favored because it offers excellent surface quality, high dimensional accuracy, and consistent thickness. Additionally, work hardening during cold rolling increases strength and surface hardness while maintaining good plasticity, making it highly suitable for stamping, bending, cabinetry, and enclosure manufacturing.
What is the neutral layer, and why is it important in unfolding calculations?
The neutral layer is the region within a bent sheet where neither tensile nor compressive stress occurs during bending. Its length remains unchanged before and after forming. This property makes it the theoretical basis for unfolding calculations, especially for thicker sheets where neutral layer theory can be applied directly.
Why is the bend deduction method recommended for thin cold-rolled steel sheets (t ≤ 3.0 mm)?
For thin cold-rolled steel sheets, neutral layer calculations become unnecessarily complex. The bend deduction method offers a simpler, empirically proven approach that delivers sufficient accuracy for angle bends, making it more practical for everyday manufacturing and shop-floor use.
How does the lower die V-groove size affect bend deduction calculations?
The lower die V-groove size directly influences the bending coefficient (Y), which determines the bend deduction (BD). Larger V-groove openings generally result in higher Y values. Standard practice uses multiples of sheet thickness (such as 6×, 8×, or 10× t), with each configuration corresponding to empirically validated Y values.
When should the 5-step arc bend calculation method be used?
The 5-step arc bend calculation method is used for arc or radius bends formed through multi-step (polygonal) bending. It is particularly effective for determining the number of bends, bend pitch, and individual bend angles, ensuring a smooth arc profile and accurate development length for complex curved sheet metal parts.

