Finding the right injection molding settings for new products often demands significant time and cost. This study introduces a reinforcement learning method that uses prior knowledge to speed up optimization. An actor-critic algorithm was applied to refine both the filling and holding phases. Tests on five different products showed that settings learned from one product (pre-learning) could effectively optimize a new one (post-learning), even with differences in material, gate design, or geometry. On average, fewer than 16 cycles were needed to optimize the filling phase and fewer than 10 for the holding phase. This approach demonstrates the potential for quicker, more efficient tuning of molding parameters and supports the development of self-adjusting injection molding systems.
Richárd Dominik Párizs, Dániel Török, ZHAOPeng ZHOUHuamin LI Yang LI Dequn
Introduction
The preferred method’s plastic injection molding process parameters have been the research hotspot of scholars. Some scholars use injection molding simulation software to optimize the molding process; however, the simulation software’s numerical computation time is long, making it difficult to meet the efficiency of the actual production [1].
Some scholars have constructed various agent models to replace the time-consuming simulation software, such as neural networks [2–3], support vector machines [4], gray system theory [5], Kriging model [6], and Gaussian process [7].
Adequate and correct learning samples are required for training to ensure the performance of the above agent models. Collecting learning samples is a vast and complex task, limiting the above models’ performance.
Collecting learning samples is a vast and complex task, which limits the application of the above models in practical production.
Many scholars have introduced artificial intelligence methods into the field of process optimization, such as Kwong et al [8], who studied the process parameter setting method based on instance reasoning;
Shelesh-Nezhad et al [9] focused on the correction strategy of instances in the process of instance reasoning; He et al [10] and Lau et al [11] proposed a fuzzy-neural model for injection process parameter setting;
Yu Bin et al [12] used rule-based fuzzy reasoning to eliminate product defects; Tan et al [13] proposed a fuzzy multi-objective optimization method for correcting product defects.
However, the case-based reasoning method has difficulty ensuring that the inferred process parameters can produce qualified products.
A purely defect-correction-based fuzzy system requires experienced process personnel to set the initial process parameters.
The fuzzy-neural model, on the other hand, requires a large number of learning samples.
These limitations result in the above research being confined to exploring principles and methodologies.
Consequently, it has not yet been able to enter the stage of practical application in engineering practice.
The relationship between injection molding machine process parameters and product quality is nonlinear, strongly coupled, and time-varying. This complexity makes it difficult to establish an accurate mathematical model.
As a result, this problem belongs to a field characterized by weak theoretical foundations and strong empirical knowledge. On the other hand, artificial intelligence and soft computing technologies are designed to model human thinking.
These technologies offer significant advantages in addressing problems within fields that are weak in theory but strong in empirical knowledge [14].
In this paper, we begin by analyzing the system characteristics of the plastic injection process. We then combine the characteristics and advantages of case-based reasoning, agent models, and fuzzy reasoning technology in handling complex problems.
Based on this, we establish a hybrid intelligent model that describes the entire process of setting and optimizing the process parameters of the injection molding machine. This model is designed to effectively simulate the thinking process of skilled craftsmen during mold trials.
It is used to intelligently set and optimize process parameters in the injection molding machine.
Hybrid intelligent modeling
When the technicians set and optimize the injection molding machine’s process parameters by the trial method, they usually first recall, compare, and learn from similar programs in the past and apply appropriate modifications as the process parameters for the first trial molding (initial process parameters).
Suppose there is no similar program to learn from. In that case, they usually make intuitive judgments based on the properties of the plastic material and the characteristics of the mold cavities, and set the initial process parameters that they think are suitable.
Then, relying on production experience and professional knowledge, the process parameters are adjusted cyclically according to the defects appearing in the trial molding process to eliminate them and obtain high-quality products.
Because of the process personnel’s idea of mold trial, this paper uses a mixture of instance reasoning, agent model, and fuzzy inference technology to establish a hybrid intelligent model for the whole process of intelligent setting and optimization of injection molding machine process parameters.
Firstly, instance reasoning and agent model technology are used to simulate the “borrowing” and “intuition” of the craftsmen to obtain the initial process parameters of the product and use them for the trial molding.
Then, fuzzy reasoning technology is used to realize the craftsmen’s process of constantly correcting defects and optimizing the process parameters. The thinking process of process parameters.
The intelligent model is divided into the initial process setting, defect correction, and process optimization. The overall framework of the innovative model is shown in Figure 1.
Initial Process Setup
Initial Process Setup Based on Example Reasoning
In actual production, cavity characteristics and plastic properties determine the size of process parameters; therefore, cavity geometry and plastic property parameters can be used as the problem characterization of instances, while qualified process parameters are used as the solution of cases.
The instance characterization is shown in Eq. (1), as follows.
Where 𝐶 = (𝐶1, 𝐶2, …, 𝐶m) is a finite set of non-empty cavity geometries, including flow length, average wall thickness, and volume;
𝑃 = (𝑃1, 𝑃2, …, 𝑃n) is a finite non-empty plastic performance parameter set, including rheological performance parameters, PVT parameters, and thermal performance parameters, etc.
𝑆 = (𝑆1, 𝑆2, …, 𝑆k) for a finite non-empty process parameter set including injection temperature, injection time, injection pressure, holding pressure, holding time, and cooling time.
The similarity between the target instance and the source instance is divided into cavity features local similarity 𝑆𝐶 (𝑖) and plastic properties local similarity 𝑆𝑃 (𝑗) In this paper, Eq. (2) is used to measure the similarity 𝑆 of the instances.
where W𝑖 and ν𝑗 are the weight coefficients. Considering that each attribute factor of sc (𝑖) and sp (𝑗) is numerical, Eq. (3) can be used to calculate each local similarity s
where 𝑥obj is the attribute factor value of the target instance; 𝑥src is the corresponding attribute factor value of the source instance; λ is the sensitivity coefficient by adjusting the size of λ and then adjusting the differentiation between the local similarities [15].
After obtaining the similarity of each source instance, the closest neighbor strategy is used for instance retrieval.
The similar instances obtained from instance retrieval need to be modified to meet the requirements of the target instance better.
Suppose the similarity between the most similar and target instances is greater than 0∙95. In that case, the most similar instance is compatible with the target instance.
The correction strategy of instance absorption is adopted, i.e., the process parameters of the most similar instance are directly used as the solution of the target instance without any correction.
If more than one similar instance meets the requirement of forming an instance matrix, then the correction strategy of the instance matrix can be adopted.
The flow length (𝐿) and the average wall thickness (𝐻) in the case of similar plastic properties reflect the problem characteristics of the target example more prominently.
Therefore, 𝐿 and 𝐻 are chosen as the horizontal and vertical axes, respectively. Process parameters such as injection pressure (𝑃inj), injection time (𝑡inj), holding pressure (𝑃hold), and having time (𝑡hold) of each similar case are taken as the functions of flow length and wall thickness to form the case coordinate system.
Fig. 2 shows the instance matrix under the instance coordinate system, and each square represents a similar instance.
The instance matrix covers the problem space within a particular flow length and wall thickness, and the solution of the target instance can be interpolated in the problem space.
If the number of similar instances is zero or the similar instances do not satisfy the conditions of both the instance sucking strategy and the instance matrix strategy, the initial process parameter setting based on instance reasoning fails.
Initial process setting based on agent modeling
In the case of failure of instance reasoning, this paper proposes an agent model based on a simplified flow model to simulate the complex relationship between product quality and process parameters, plastic properties, and cavity characteristics, and set the initial process parameters according to specific preference criteria.
Cavity pressure, melt temperature difference, and injection time are important parameters affecting product quality and production efficiency [16]. These factors must be carefully controlled.
During the molding process, the cavity pressure should be kept as low as possible, and the melt temperature should remain uniform and consistent.
When the difference in product quality is small, a shorter injection time can help improve production efficiency. Equation (4) shows the corresponding optimization model.
Where 𝑋 is the design variable, defined process parameters, including injection temperature 𝑡0, mold temperature 𝑡w, and injection time tinj, 𝑋Lk and 𝑋Uk are the lower and upper bounds of the design variable, respectively;
𝑃cavity, Δ𝑡m, and tinj are the optimization objective values, representing the cavity pressure, melt temperature difference, and injection time, respectively. To eliminate the magnitude effect, each optimization objective value is normalized to between [0, 1].
𝑤1, 𝑤2, 𝑤3 are weight coefficients of the value according to the importance of each optimization objective to determine.
Most plastic parts are thin-walled products with uniform wall thickness. The cavity’s maximum flow length and average wall thickness are determined according to the cavity’s geometric characteristics and the gate’s location.
The cavity is simplified for products with complex cavities into a rectangular flat plate with a gate at the end. This simplification is based on the principle of volume equality.
Introducing reasonable assumptions and simplification conditions from the basic equations of viscous fluid dynamics can be derived from the simplified flow model of the control equation
Where 𝑢 is the flow rate in 𝑥-direction, 𝑃, 𝑇, 𝑡 and 𝑄 denote the pressure, temperature, time and flow rate η, ρ, 𝑐p and 𝐾 are the melt viscosity, density, specific heat capacity and thermal conductivity respectively, and 𝑊 and 𝐻 are the equivalent width and thickness of the cavity respectively.
This paper uses the finite difference method to solve the above control equations and predict the cavity pressure and melt temperature difference at the end of the injection [17].
A differential discretization grid is introduced in the cavity wall thickness direction (𝑧-direction) and the flow direction (𝑥-direction), assuming that the melt flow is symmetric with respect to the center of the cavity (𝑧 = 0). Only the flow process in the upper half of the center layer is considered.
In the windward format, a backward differential in the flow direction is used, while the wall thickness direction is used in the center differential format.
The backward difference in the windward direction is used for the flow direction, and the center difference format is used for the wall thickness direction.
The initial process parameters obtained based on example reasoning or an agent model are theoretical parameters, which need to be converted into machine parameters that can be recognized by the injection molding machine according to its structure and specifications.
Defect Correction and Process Optimization
In the mold trial process, the product may have multiple defects 𝐷𝑖 (𝑖 = 1, 2, …, 𝑚) at the same time. The correction of defects 𝐷𝑖 requires the adjustment of one or more process parameters where 𝑃𝑗, (𝑗 = 1, 2, …, 𝑛).
The type of defects determines the direction of the process parameter adjustment, and the amount of adjustment Δ𝑃𝑗 is affected by the degree of defects and the size of the process parameter (process parameter size) in the last mold trial process.
The defect type determines the direction of process parameter adjustment, and its adjustment amount Δ𝑃𝑗 is constrained by the defect degree and the size of the process parameter in the last mold trial process (current value of the process parameter).
In this paper, a knowledge-based fuzzy inference system is established to optimize the process parameters to realize the intelligent correction of product defects. The adjustment direction of the process parameters is judged by rule-based reasoning, while the fuzzy inference machine is used to solve the adjustment amplitude of the process parameters.
Fig. 3 shows the computational framework for defect correction and process optimization. The type and degree of defects and the current values of process parameters are inputs to the fuzzy inference system.
The adjustment amount of process parameters is taken as the output of the fuzzy inference system, which adopts the ” divide-and-conquer ” strategy for multiple defects, and ultimately carries out conflict elimination and merging to obtain the comprehensive adjustment amount of process parameters for each defect.
The system adopts a “divide and conquer” strategy for multiple defects, and finally performs conflict elimination and merging to get the integrated adjustment amount of each process parameter.
Fig. 3 Calculation box for defect correction and process optimization.
In the figure, “adjustor 𝑖 𝑗 represents the fuzzy inference subsystem that implements the adjustment of process parameters 𝑃𝑗 by defect 𝐷𝑖.
Design of fuzzy rules
The fuzzy inference system uses fuzzy if-then rules of the following form:
if 𝑥 is 𝐴 and 𝑦 is 𝐵 then 𝑧 is 𝐶.
Where 𝑥 is the linguistic variable “degree of defect”, 𝑦 is the linguistic variable “size of the current value of the process parameter”, 𝑧 is the linguistic variable “magnitude of the adjustment of the process parameter”, and 𝐴, 𝐵 and 𝐶 are the domains 𝑋, 𝑌 and 𝑍, respectively. 𝐴, 𝐵, and 𝐶 are the linguistic values defined on the domains 𝑋, 𝑌, and 𝑍, respectively.
𝐴 describes the degree of defects, the set of terms is ｛Severe, Medium, Slight｝;
𝐵 describes the size of the current value of the process parameter with the term set {large, medium, small};
𝐶 describes the magnitude of the process parameter adjustment with the terminology set of ｛Large, Large, Large, Medium, Small, Small, Small｝.
To comply with the human mind’s intuitive understanding of the division of the input space, the parameterized triangular affiliation function, as shown in equation (8), is used to define the linguistic values in the set of terms.
Fuzzy inference mechanism
The fuzzy inference system adopts the inference form of “multiple antecedents and multiple rules” and uses the Mamdani fuzzy inference model [14], which uses the very large-very small operator as the T-paradigm and T-co-paradigm operator. Its inference process is shown in Fig. 4.
As mentioned before, the meaning of the symbols in the rules is that C′ is the linguistic value describing the final adjustment amplitude of the process parameters, 𝑧 is the parameter adjustment amplitude, and 𝑧 is the linguistic value of the parameter adjustment amplitude.
Linguistic value, 𝑧 is the exact value of the parameter adjustment magnitude, 𝑥 = A′ or x0, 𝑦 = 𝑦0 are facts, i.e., model inputs.
For a single fuzzy rule, “A𝑘 × B𝑘 → C𝑘”, can be converted into a ternary fuzzy relation 𝑅𝑘 based on fuzzy implicit function expression
R𝑘 (A𝑘, B𝑘, C𝑘) =
The inference result C′, k of a single fuzzy rule can be expressed as
For the case of multiple rules, the inference model agglomerates the results obtained from the inference of a single rule, and the output fuzzy set expresses the adjustment of the process parameters
The output fuzzy set C′ needs to be defuzzified to obtain the exact value z of the adjustment amplitude of the process parameters, which is solved by using the center of area method ZCOA in this paper.
System Verification
According to the above model and method, the intelligent setting and optimization system of plastic injection process parameters is developed under the Microsoft Visual C++ compilation environment.
It is programmed with Winsock and communicates with the controller using the standard TCP/IP communication interface on the injection molding machine controller to integrate with the injection molding machine.
Validation of the simplified flow model
The predicted results of the simplified flow model include the cavity pressure and melt temperature difference, where the cavity pressure is easy to measure, and the melt temperature difference is difficult to measure. In this paper, the correctness of the simplified flow model is verified by comparing the predicted value of the cavity pressure at the end of the injection with the experimental value.
As shown in Fig. 5, the experimental mold cavity is a rectangular box; its maximum flow length is 110.0 mm, the average wall thickness is 2.6 mm, and it uses direct gating, which is marked as “●”, the location of the melt pressure test point (pressure sensor location).
GPPS was chosen as the experimental material, and its corresponding material parameters ρ, 𝐶p, and 𝐾 were 954.12 kg∙m-3, 1700 J∙kg-1∙°C-1, and 0∙14W∙m-1∙°C -1. The relevant parameters 𝑛, τ∗, 𝐷1, 𝐷2, 𝐷3, 𝐴1, and 𝐴2 for the viscosity 7-parameter model are 0.1, 61400 Pa, 2∙32×109 Pa∙s, 373.15 K, 0 K∙Pa-1, 21.363 K, and 51.6 K, respectively.
Fig. 6 shows the finite difference mesh constructed for this experiment. The number of meshes in the thickness and length directions is 8 and 100, respectively.
Table 1 compares the simplified flow model’s predicted and experimental cavity pressure values under different process parameters.
The predicted values of the cavity pressure agree well with the experimental values, and the relative error limit is only 8.41%, so it is practical to use the simplified flow model as a surrogate model for setting the initial process.
Functional verification of the system
To verify the overall function of the system, the actual products of a mold enterprise are selected for experimentation.
Fig. 7 shows the products. The cavity volume is 13.9cm3, the flow length is 180.55mm, and the average wall thickness is 1.71mm. The plastic material is PP, and the injection molding machine model is HTL140.
The similarity threshold is set to 0.85, no similar instance is retrieved, and instance reasoning fails.
The injection and mold temperatures adopt the recommended material values: 230 ℃ and 50 ℃, respectively. A simplified flow model is constructed by searching for the minimum value of the optimization objective function.
As a result, the preferred injection time is determined to be 1.4 s. Based on simplified flow model calculations, the required injection pressure under the above process parameters is 15.0 MPa. The initial values of the primary process parameters are shown in Table 2.
After the first trial molding, the product showed moderate “under-injection” defects. The user provided feedback on the type and degree of the defects.
Based on this feedback, fuzzy reasoning was applied to obtain the first set of adjusted process parameters (Table 2). These parameters were then uploaded to the injection molding machine controller.
Afterward, the mold was tried again. This time, a slight “flying edge” defect appeared. The user again provided feedback on the type and severity of the defect. Once more, fuzzy reasoning was used to obtain a second set of adjusted process parameters (Table 2).
These new parameters were uploaded to the controller for another trial molding.
As a result, the “flying edge” defects were eliminated. The product was qualified, and the optimized process parameters were obtained.
Figure 7 (a) to (c) shows the sequence of three products from each trial molding. Figures 7 (a), (b), and (c) correspond to the first, second, and third trial mold products, respectively.
System performance verification
The case is a mold enterprise that produces 10L lubricating oil drum plastic material for PP, one mold, one cavity, using direct gating. The product quality is 398.0g, the average wall thickness is 1.5mm, and the flow length is 368.0mm, using an injection molding machine model HTW730B.
The craftsmen tried 15 molds to obtain qualified products successfully, and the intelligent system used only 2 molds to obtain qualified products successfully.
Figure 8 shows the final product obtained by the two methods.
Due to the unreasonable setting of holding pressure parameters, the final product obtained by manual molding shows noticeable shrinkage marks.
In contrast, the final product obtained by the intelligent system has a uniform wall thickness and appears complete. Its overall quality is better than that obtained by manual molding.
Conclusion
The traditional method of setting process parameters of injection molding machines is mainly a trying method, leading to long production cycles, high costs, and difficulty guaranteeing product quality.
In this paper, a hybrid intelligent model describing the complete process of setting process parameters and optimizing injection molding machines is established for the process personnel’s trying thinking.
It combines the advantages of instance reasoning, agent model, and fuzzy reasoning technology in dealing with problems in the weak theory and strong experience field.
Instance reasoning to solve problems is in line with processors’ thinking to recall, compare, and draw on similar solutions in the past when setting up the initial process, which can be used to set up the injection molding machine’s initial process parameters.
Cavity pressure and melt temperature difference are two essential quality indicators reflecting the quality of injection molding products.
The simplified flow model is used as an agent model, and the process parameters are preferred based on specific optimization criteria to realize the setting of initial process parameters of the injection molding machine when instance reasoning fails.
Fuzzy inference technology is a computational tool that represents knowledge and information in natural language, which is suitable for solving problems where the degree of defects in the defect correction process often cannot be described precisely.
Actual production cases show that the intelligent setting and optimization system for plastic injection process parameters, developed based on the above model, can automatically set the process parameters of the injection molding machine.
It can also intelligently eliminate product defects. Compared with the traditional “trying method” based on experience, the intelligent system greatly shortens the cycle of process setting.
It also reduces production costs. In addition, it improves the quality of the products. Product quality is significantly enhanced through this intelligent approach.
Injection molding Case
Various factors, including mold structure, injection parameters, and production environment influence the molding quality of plastic parts.
Due to the characteristics of plastics and the complexity of processing equipment, injection molding is a highly complicated process; however, the influence of injection parameters on the quality of plastic parts is crucial.
Before production, it is necessary to adjust the machine injection molding to obtain the quality of qualified plastic parts, which is a process that consumes a lot of labor and material costs.
The rise of computer-aided engineering (CAE) has solved the problem of cost, transforming the actual injection molding process into a CAE simulation on the computer, and optimizing injection parameters through mold flow analysis, thereby realizing zero-cost testing of injection molding debugging.
However, there are many variables in the injection molding process, such as barrel temperature, mold temperature, and injection time, among others, and each injection parameter is related to the others within the injection molding process.
Coupled with the evaluation of the quality of plastic parts and a lot of indicators, different evaluation indicators to adapt to the use of various plastic parts requirements, and how to choose a reasonable combination of injection molding parameters to get a better quality of plastic parts is a problem that injection molding enterprises need to solve.
If the combination of injection molding parameters is chosen by experience, firstly, the experience level of technicians is required to be high;
Secondly, a large number of experimental tests are required to compare the better quality plastic parts, and the specific influence of the parameters on the quality indexes cannot be clearly observed, resulting in a rather vague effect.
Thirdly, we cannot obtain the best combination of parameters solely from the parameters that have been debugged to choose the best one, and the effect of the combination of parameters that have not been tested cannot be reflected.
The introduction of orthogonal test, through the rational design of the test list, the scientific design of test combinations, that is, a small number of typical process parameter combinations can be derived from the analysis of the test results reflecting the full range of information including the parameter combinations that have not done the test, to avoid disorderly groping for the test, to find the best parameter combinations;
And can find the test quality indicators of the influence of the larger factors of the process parameters, in the adjustment of the machine to make key adjustments.
Plastic analysis
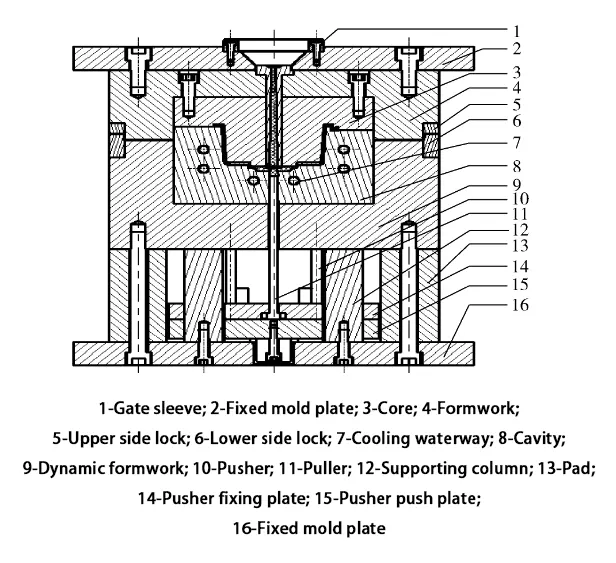
Figure 1 shows a car with an organizer box. There are depressions for loading. The surface requires smoothness and no traces, so the conventional mold structure cannot be used to avoid the pusher leaving traces on it.
To solve the mold demolding problem, but not to increase the mold structure to avoid cost increases, the use of inverted mold structure, i.e., the core installed in the fixed mold, cavity installed in the moving mold, the top of the pusher in the plastic than the surface of the surface, the use of the surface has no effect;
To ensure that the mold can follow the moving mold when the mold is opened, a grid pattern is designed on the outside of the plastic part, and the connecting force between the pattern and the cavity is used to pull out the plastic part; and the square hole in the middle is used to set up a double gate for feeding the material;
A three-dimensional cooling system is used to surround the inner and outer surfaces of the part. The mesh model established in Moldflow is shown in Fig. 2, and the material used is acrylonitrile-butadiene-styrene copolymer (ABS) of grade 728-A from Kumho Petrochemical Company in South Korea. This material has a good luster and coloring, making it suitable for the aesthetics of automobile interior parts. It is ideal for the aesthetics of automobile interior parts.
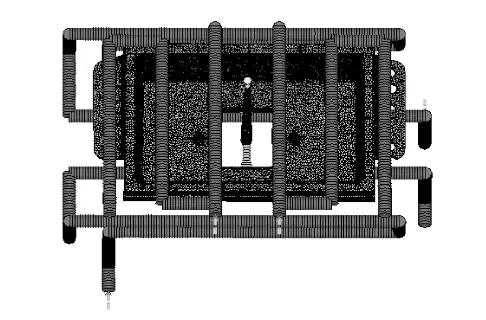
From the point of view of the use and assembly of the organizer box, it does not need to withstand too much force, but there are specific requirements for the assembly precision, when assembling the plastic parts in the length direction, i.e., the 𝑦 direction, the 𝑥 direction and the z direction have no limitations, therefore, the volumetric shrinkage of the plastic parts and the warping deformation in the 𝑦 direction are used as the test indexes of the plastic parts, and the smaller the smaller indicates the higher dimensional precision of the plastic parts: the smaller the dimension, the higher the dimensional accuracy of the plastic part.
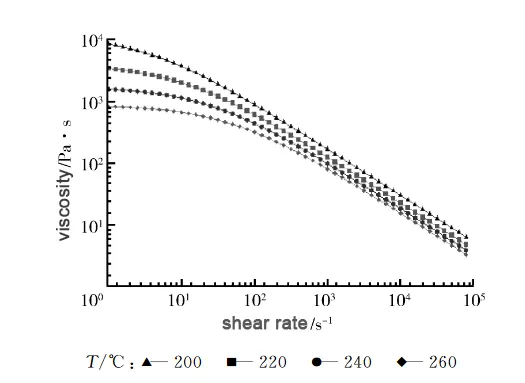
Figure 3 shows the viscosity characteristic curve of plastic materials, from which it can be seen that the plastic raw materials exhibit different viscosity characteristics at various melt temperatures and shear rates, which directly affect the melt flow filling process during injection molding.
According to the influencing factors of melt viscosity, the injection rate (characterized by injection time), mold temperature and melt temperature were taken as the test factors;
According to the influencing factors of molding shrinkage of plastic parts, the test factors included holding time, holding pressure (characterized by the percentage of injection pressure), and cooling time.
Orthogonal test
Design of test factors and levels
The recommended process parameters of ABS materials in Moldflow are shown in Table 1. Then according to a certain amount of simulation analysis results and practical experience, the orthogonal test factors and levels are formulated as shown in Table 2, the test factors for the melt temperature, mold temperature, injection time, holding pressure and cooling time of the five factors, divided into four levels of settings, the holding time is set at a uniform 10s.
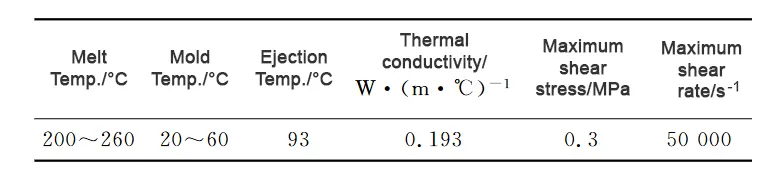
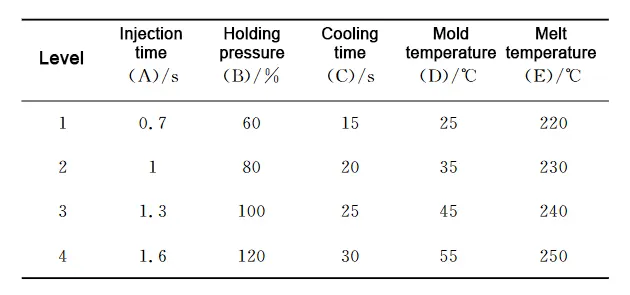
The test standard measures volumetric shrinkage and warping deformation in the 𝑦 direction; the smaller the standard value, the better the quality of the plastic parts.
Test the factor combination program and standardized value results
According to the five-factor four-level design test factor combination L9 (33) orthogonal test table, as shown in Table 3, the results of the test standard value obtained for each row of the injection molding parameter combination scheme for CAE mode flow analysis will be recorded in Table 3 as well.
Volumetric shrinkage and its extreme difference analysis
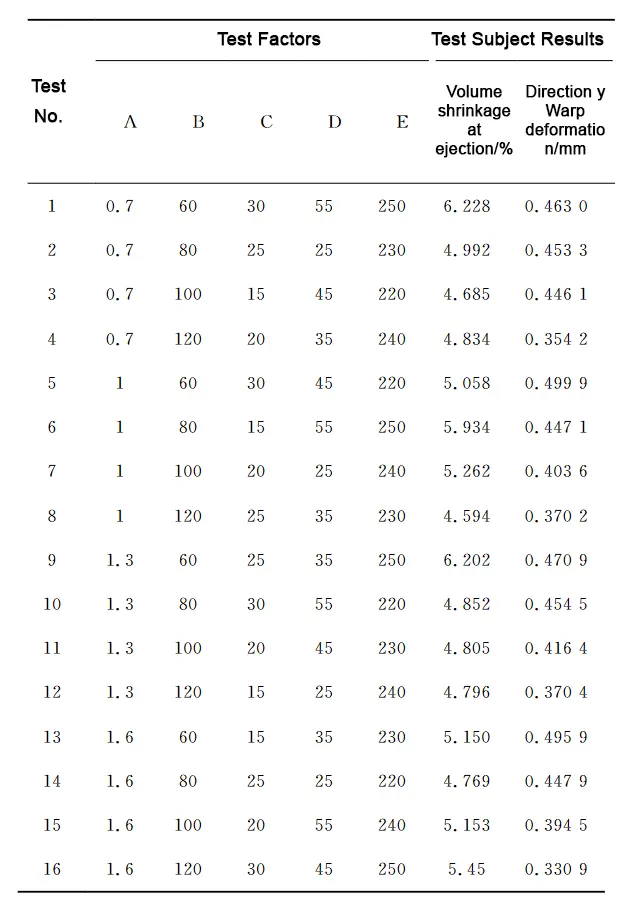
The values of volumetric shrinkage in Table 3 are transformed into mean values and analyzed for polar deviation at different levels of factors, as shown in Table 4, to examine the effect of each factor level on the volumetric shrinkage of plastic parts.
The extreme deviation Rj in Table 4 characterizes the influence of each factor on the volume shrinkage rate of plastic parts. As can be seen from Table 4, the order of extreme deviation is as follows:
Melt temperature (1.113) > Holding pressure (0.742) > Mold temperature (0.587) > Cooling time (0.384) > Injection time (0.081).
The melt temperature had the most significant effect on the volume shrinkage rate, while holding pressure, mold temperature, and cooling time had the second most considerable effect, and injection time had the least impact.
Therefore, when the theoretical optimization value is obtained, the melt temperature and holding pressure should be fine-tuned as a priority in the actual injection molding machine, to achieve better and faster mold trial success.
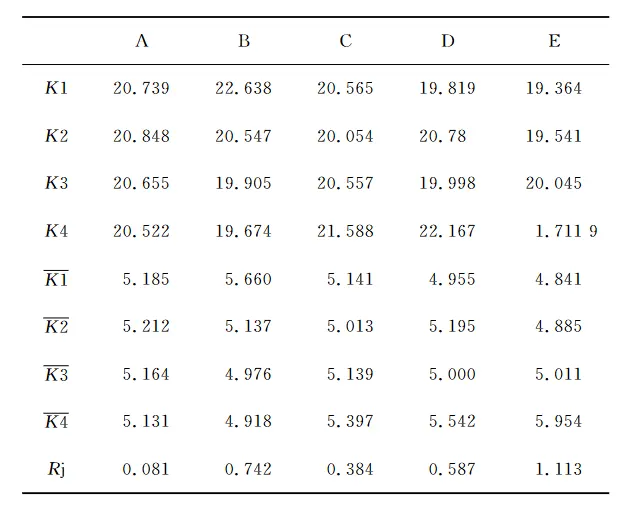
To characterize the effect of each level on the volumetric shrinkage rate, the horizontal span of each factor is taken as the horizontal coordinate of Fig. 4. The corresponding value of volumetric shrinkage rate is taken as the vertical coordinate. The trend graph of the effect of the horizontal span of each factor on the volumetric shrinkage rate of the plastic part is drawn, as shown in Fig. 4.
As can be seen from the figure, the effect of the injection time of factor A on the volumetric shrinkage rate tends to be flat, with little impact. The volumetric shrinkage rate decreases slightly when the injection time is increased to 1.6 seconds.
The effect of injection time on the volumetric shrinkage rate of factor B is also shown in the figure.
The B factor, which is the increase in holding pressure, significantly decreases the volume shrinkage rate. This indicates that sufficient holding pressure helps reduce the volume shrinkage rate, as the rise in holding pressure makes the plastic part more compact, leading to a reduction in the shrinkage space of the plastic part.
C. The increase of cooling time leads to the decrease of volume shrinkage rate firstly and then increases, which shows that both insufficient and too long cooling time are not desirable, and the cooling time of 20s is more suitable.
D. factor mold temperature at low temperature volumetric shrinkage rate is small, when the mold temperature increases to 55 ℃, the volumetric shrinkage rate increases significantly; lower mold temperature is conducive to reducing the volumetric shrinkage rate of plastic parts.
At the same time, the volume shrinkage rate also with the E factor melt temperature increases up, in 200 ℃ to 240 ℃ when the slope is smaller, the volume shrinkage rate increases more slowly, and then continue to rise to 250 ℃, the rate of increase is larger, indicating that the melt temperature is not suitable for too high.
𝑦 Directional warpage deformation and its polar analysis
The storage box has assembly requirements in the 𝑦 direction, so the warpage deformation in the 𝑦 direction has higher standards, and there are no high requirements for the 𝑥 and 𝑧 directions.
The warpage deformation in the 𝑦 direction in Table 2 is transformed into a mean value and solved for the extreme deviation under different factor levels, as shown in Table 5. The impact of the various levels on the 𝑦 direction of the plastic part is then analyzed.
Table 5 analyzes the influence of each level factor on the variation of warpage deformation in the 𝑦 direction of the plastic part.
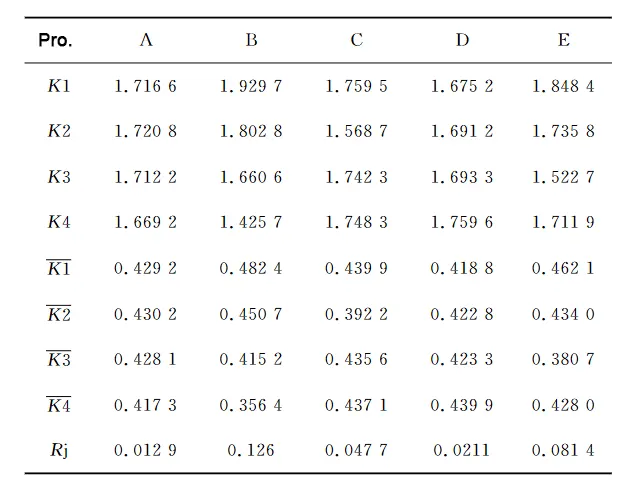
The extreme deviation Rj in Table 5 characterizes the influence of each factor on the warpage deformation of plastic parts in 𝑦 direction, and it can be seen from Table 5 that the extreme deviations are in the following order:
Holding pressure (0.126) > melt temperature (0.0814) > cooling time (0.0477) > mold temperature (0.0211) > injection time (0.0129).
Holding pressure on the 𝑦 direction of warpage deformation of the most significant impact, the influence of the melt temperature is followed by the cooling time and mold temperature, and again, the influence of the injection time is minimal.
Therefore, it is preferable to prioritize the two parameters of holding pressure and melt temperature when tuning the machine, which agrees with the tuning of volumetric shrinkage.
Similarly, the level span of each factor is taken as the horizontal coordinate, and the corresponding value of warpage deformation in the direction of y is taken as the vertical coordinate; the trend of change is plotted as shown in Fig. 5.
From the figure, it can be seen that the intuitive changes in the effect of the level of each factor on the amount of warpage deformation in the 𝑦 direction of the plastic part.
The curve of the A factor injection time is almost a horizontal straight line, indicating that the effect of injection time is negligible, and the decrease of warpage deformation in the 𝑦 direction with the increase of injection time is limited.
B factor holding pressure has the most significant effect, and sufficient holding pressure can significantly reduce the warpage in the 𝑦 direction, and the curve shows a decreasing trend.
C factor cooling time and E factor melt temperature on 𝑦-direction warpage deformation are both decreasing and then increasing, indicating that the cooling time of 20s and the melt temperature of 240 ℃ are the reasonable parameter choices, and both too high and too low will cause the 𝑦-direction warpage to increase;
The D factor mold temperature also has a negligible effect on the plastic parts, primarily at the D4 level, where a slight increase is observed, and overall, a small upward trend is shown, indicating a minimal increase in the trend.
Comprehensive analysis
Take the lowest point of each curve in Fig. 4 to get the process parameter combination A4B4C2D1E1 when the volume shrinkage rate is the smallest, and take the lowest point of each curve in Fig. 5 to get the process parameter combination A4B4C2D1E3 when the warping and deformation of the 𝑦 direction is the smallest, the values of the process parameter of the two cases are generally the same, but only there is a disagreement in the E factor.
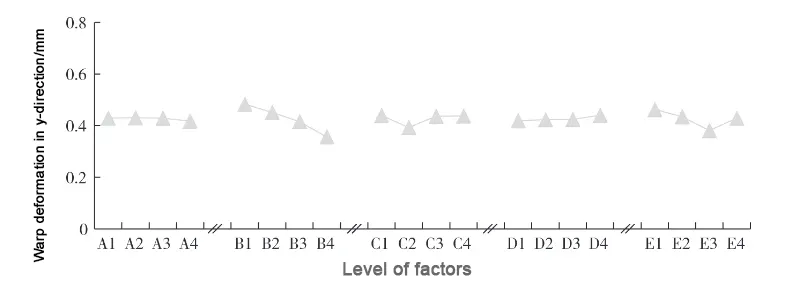
From the comparison of the two figures, if E1 is chosen as the E factor, the warping deformation in the 𝑦 direction increases by (0.4621-0.3807)/0.3807 = 21.4% compared with that of E3;
If E3 is chosen as the E factor, the volumetric shrinkage increases by (5.011-4.841)/4.841 = 3.5% compared to E1.
Meanwhile, since 𝑦-directional warpage deformation is the primary factor affecting assembly accuracy, volume shrinkage is more pronounced throughout the entire body.
To summarize the above reasons, it is evident that E3 is the better choice; therefore, the optimal combination of process parameters is A4B4C2D1E3.
Because this process combination is not included in the experimental combinations in Table 3, set the corresponding parameters in Moldflow and then perform a modeling analysis to view the results, as shown in Figs. 6 to 13.
Fig.6 shows that the maximum volumetric shrinkage rate is 4.703%, which is not the smallest value in Table 2, but it is still small, and it is controlled within 5%, and the overall shrinkage rate is not significant.
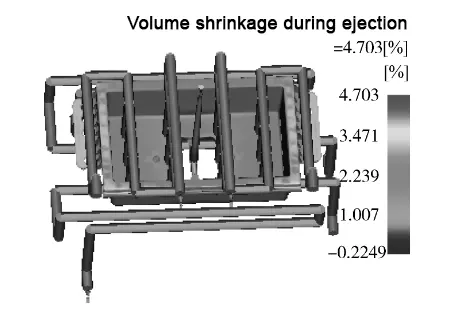
Fig. 7 shows that the maximum warpage deformation in the direction of 𝑦 under all factors is 0.3298 mm, which is smaller than the minimum value in Table 2, indicating an optimal result.
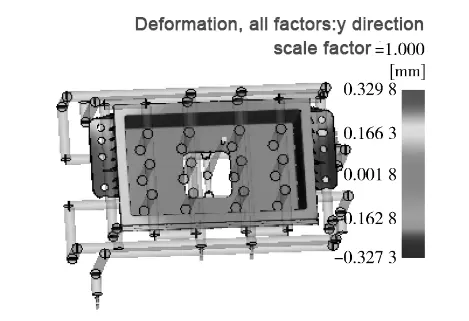
Fig. 8 Filling time shows that the latest filling place of the plastic part is at the two ears and the bottom hole, which is the thinnest part of the whole plastic part, and conforms to the principle of filling.
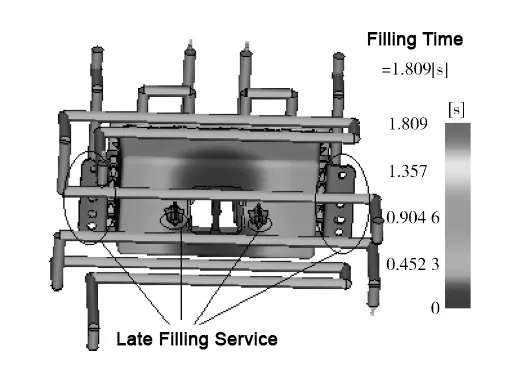
Fig. 9 shows the possible cavitation positions during the filling process; all of them are concentrated at the parting surface of the mold. This means that it is possible to utilize the gap of the parting surface of the mold for ventilation, or to open venting slots at the corresponding locations.
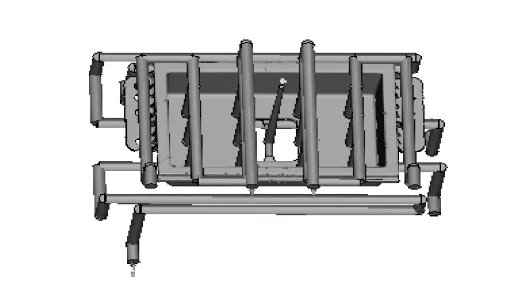
Fig. 10 shows that the estimation of cavitation indicates that the cavitation value is essentially controlled at around 40 μm, resulting in an excellent surface quality of the molded part. Fig. 11 of the circuit cooling liquid temperature shows that the temperature difference between the inlet and outlet water temperatures is 1.63 ℃;
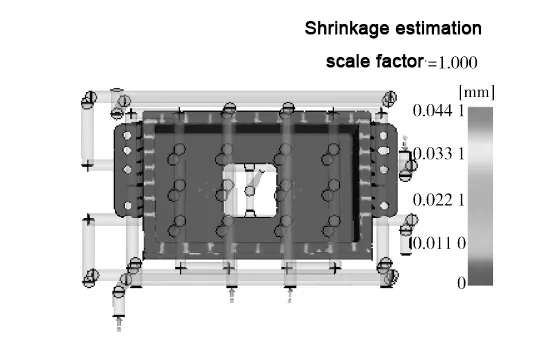
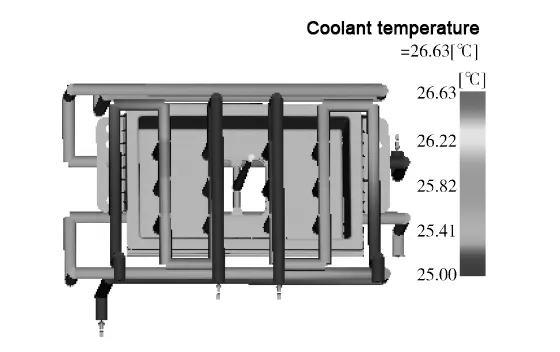
Fig. 12 shows the melt flow front temperature when filling the cavity, except for the bottom two holes of the molded part, due to the thin wal,l and the latest filling temperature is slightly lower, the other parts of the filling temperature is the same.
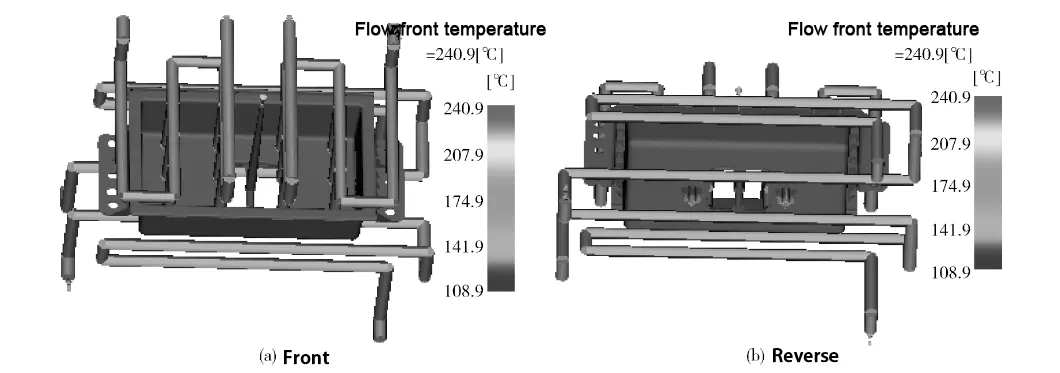
Fig.13 shows that the cooling of the molded part is more uniform, the temperature field distribution after pressure preservation cooling is also more uniform, the temperature difference between the inner and outer areas of the molded part is basically within 10 ℃, and the cooling effect is perfect.
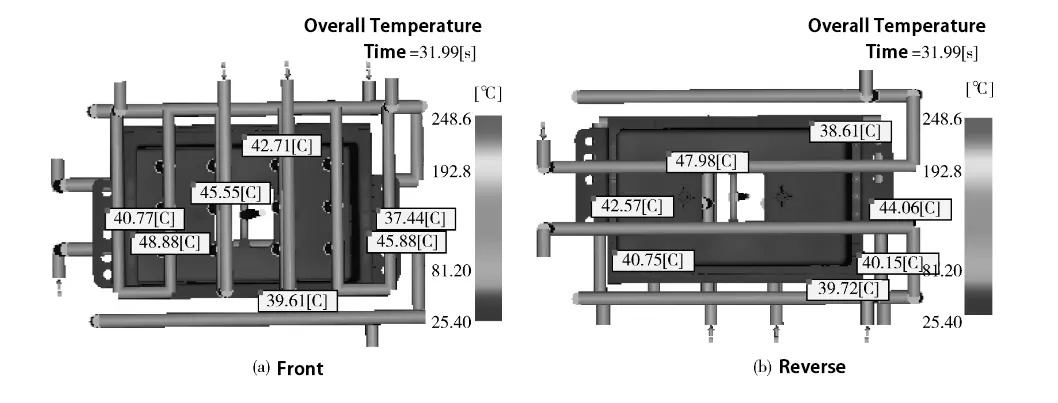
Production Verification
According to the mold structure shown in Figure 14 for mold manufacturing and based on the results of the above analysis for the trial mold, the material used in South Korea Kumho 728-A grade acrylonitrile – butadiene – styrene copolymer (ABS), debugging to maintain the injection time of 1.6s, holding pressure of 120% (4.7.25MPa), cooling time of 20s, mold temperature 25 ℃ and melt temperature 240 ℃ constant. 7.25MPa), cooling time of 20s, mold temperature of 25 ℃ and melt temperature of 240 ℃ unchanged, and adjust the screw back pressure appropriately.
The production of the organizer products, as shown in Figure 15, after testing, the length of the plastic body shows a shrinkage rate of 4.82%, the width of the shrinkage rate of 4.69%, the height of the shrinkage rate of 4.71%, and the average shrinkage rate of 4.74%.
𝑦 Direction warping deformation 0.331mm, the value and the theoretical optimization value are not much different, which belongs to the reasonable deviation range, the factory inspection meets the manufacturer’s production requirements, and ensures smooth delivery.
Conclusion
(1) Through the orthogonal test and mold flow analysis on the automobile stowage box injection molding production of the tuning parameters for optimization tests, affecting the use of the stowage box assembly is mainly the volume shrinkage rate and 𝑦 direction warping deformation, the production of the best injection molding process parameter combinations are obtained as follows:
Injection time 1.6s, holding pressure 120%, cooling time 20s, mold temperature 25 ℃, and melt temperature 240 ℃, after the production of evidence, the production of products manufacturers’ smooth acceptance;
(2) Through the orthogonal test and mold flow analysis, the trend of the influence of each process parameter on the volume shrinkage rate and 𝑦-directional warpage and deformation was obtained, and the results showed that the holding pressure and melt temperature were the ones that had more influence on these two plastic performance indexes, and the testing of these two parameters should be prioritized in the setting up of injection molding machine;
(3) the use of orthogonal test can be obtained for different performance indicators of various parameters of the trend, can be targeted to efficiently achieve the adjustment of a performance indicator of the parameter tuning of the plastic parts, to promote the digital design of products to drive the high quality development of low-cost innovation, in the plastics industry and mold enterprises have a wide range of popularization value.